EDR 距离 （Edit Distance on Real Sequence）

详见paper

• Robust and Fast Similarity Search for Moving Object Trajectory

基本思想

对于两个时间序列，例如轨迹序列，两序列间的相似度距离为 一个序列转化为另一个序列所需要要的最小操作次数。对于序列中的元素点（轨迹采样点），如果这两个采样点各个维度的差值均不超过一个给定的阈值限制 epsilon，我们认为这两个点可以匹配，这两个采样点间距离为0，即操作距离为0. 如果这两个采样点某个维度的差值超过一个给定的阈值限制 epsilon， 我们认为这两个点不可以匹配，这两个采样点间距离为1，即操作距离为1. 至少需要一次操作才能将其中一条轨迹转化为另一条。

• e.g. Q = (1,2,3,4), S=(1,100,2,3,4) ，epsilon=1 其两两点间的操作距离subcost 如下：
  -
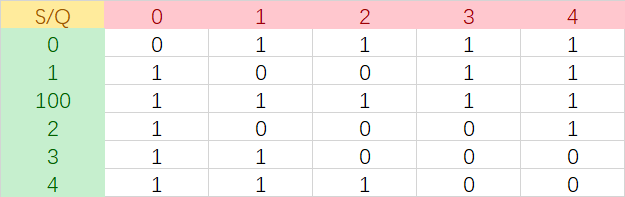
  找一条从该矩阵(0,0)到（m,n)的最短路即为两条时间序列的EDR距离，距离越小则相似度越大。这就是基本的思想。其中，m，n为序列S,Q的长度。矩阵中添加一个0是考虑序列为空的情况。具体来说，递归式如下：
  

该距离量化方法的优点

• 可以避免噪声数据对距离刻画产生的巨大影响，两点不匹配均用距离1来刻画
• 可以处理长度不一的序列，能够处理 local time shifting
• 距离是对称的 （metric), EDR(R,S) = EDR(S,R)

实际操作中注意事项

• 对数据点每个维度进行适当的归一化操作
• 时间复杂度为 O(n^2)
• 需要使用一些高效的修剪枝技术来提高运算效率

Java 实现EDR距离

以int 数据类型为例， 示例中设置 epsilon = 1

package precomputation;

import java.util.ArrayList;
import java.util.Arrays;

public class EDR {
	
	public static void main(String[] args) {
		int[] Q= {1,2,3,4};
		int[] S= {1,100,2,3,4};
		int ep = 1;
		int[][] res = EDR2(Q,S,ep);
		System.out.println(Arrays.deepToString(res));
		
	}
	

	/*
	 * 方式1：直接动态规划计算，需要设置很多判断条件
	 * 方式2：先计算subcost 0，1矩阵，在01矩阵上做动态规划找一条最短路径即可，更为简单容易理解
	 * 以int类型数组为例, EDR(Q,S)=EDR(S,Q)是对称的
	 * 在实际应用中，可能还需要涉及到 数据维度归一化的一些操作
	 */
	public static int[][] EDR1(int[] seq1, int[] seq2, int epsilon)
	{
		int m = seq1.length;
		int n = seq2.length;
		// 建立dp矩阵
		int[][] dp = new int[m+1][n+1];
		// 初始化第一行，第一列
		for(int i=0;i<n+1;i++)
		{
			dp[0][i] = i;
		}
		for(int i=0;i<m+1;i++)
		{
			dp[i][0] = i;
		}
		// 开始动态规划, 时间复杂度O(n^2)
		for(int i=1;i<m+1;i++)
		{
			for(int j=1;j<n+1;j++)
			{
				int subcost = Math.abs(seq1[i-1]-seq2[j-1])<=epsilon ? 0:1;
				int min = Math.min(dp[i-1][j-1]+subcost, dp[i][j-1]+1);
				min = Math.min(min, dp[i][j-1]+1);
				dp[i][j] = min;
			}
		}
		return dp;
	}
	
	public static int[][] EDR2(int[] seq1, int[] seq2, int epsilon)
	{
		int m = seq1.length;
		int n = seq2.length;
		// 建立01矩阵计算两两间的subcost
		int[][] subcosts = new int[m+1][n+1];
		// 初始化第一行，第一列
		subcosts[0][0] = 0;
		for(int i=1;i<n+1;i++)
		{
			subcosts[0][i] = 1;
		}
		for(int i=1;i<m+1;i++)
		{
			subcosts[i][0] = 1;
		}
		// 计算两两间的subcost
		for(int i=1;i<m+1;i++)
		{
			for(int j=1;j<n+1;j++)
			{
				subcosts[i][j] = Math.abs(seq1[i-1]-seq2[j-1])<=epsilon ? 0:1;
			}
		}
		// 建立dp矩阵, 在subcosts 01矩阵上做动态规划找一条最短路径即可
		int[][] dp = new int[m+1][n+1];
		for(int i=0;i<n+1;i++)
		{
			dp[0][i] = i;
		}
		for(int i=0;i<m+1;i++)
		{
			dp[i][0] = i;
		}
		for(int i=1;i<m+1;i++)
		{
			for(int j=1;j<n+1;j++)
			{
				int min = Math.min(dp[i-1][j-1]+subcosts[i][j], dp[i][j-1]+1);
				min = Math.min(min, dp[i][j-1]+1);
				dp[i][j] = min;
			}
		}
		return dp;
	}
	
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100